표준오차의 뜻과 정의
표준오차(Standard Error, SE)는 통계에서 표본 평균의 변동성을 측정하는 지표입니다. 이는 표본 평균이 모집단 평균에 얼마나 가까운지를 나타내며, 통계적 추정치의 불확실성을 평가하는 데 사용됩니다.
모집단의 평균을 추정하는 것은 표본평균이고 이 표본평균들의 변동성 즉 표준편차를 표준오차라고 함.. 이는 개별 데이터 대신 통계량의 변동성을 측정하는 것일 뿐임

주요 특징과 정의
표본 분포의 표준편차
표준오차는 표본 평균 분포의 표준편차로 정의됩니다. 이는 모집단의 표준편차를 표본 크기의 제곱근으로 나눈 값으로 계산됩니다.
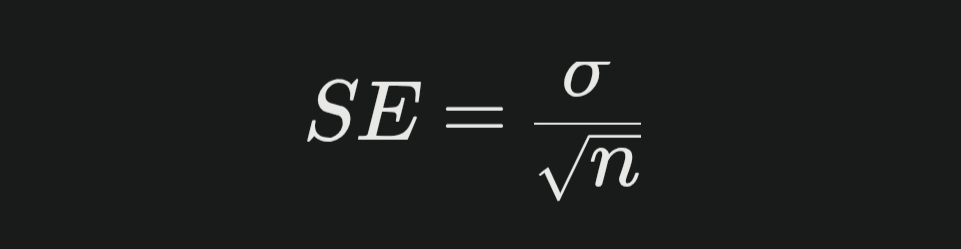
표본 크기와 관계
표본 크기가 커질수록 표준오차는 작아집니다. 이는 더 큰 표본이 모집단을 더 정확히 대표하기 때문입니다.
통계적 의미
표준오차가 작을수록 추정치의 변동성이 적고, 신뢰구간이 좁아져 추정치가 더 정확해집니다. 반대로, 표준오차가 클수록 추정치의 불확실성이 증가합니다.
신뢰구간에 활용
신뢰구간은 표준오차를 이용하여 다음과 같은 방식으로 계산됩니다.
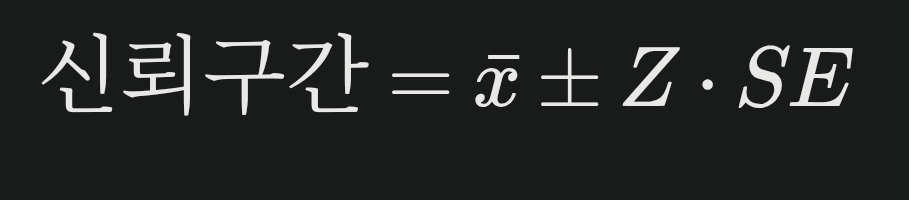
예측 모델링 및 데이터 분석:
표준오차는 통계적 예측 모델에서 결과의 오차를 측정하거나 데이터 분석에서 추정치의 정확도를 평가하는 데 사용됩니다.
중심극한정리와 관련성
중심극한정리에 따르면, 충분히 큰 표본 크기에서는 표본 평균 분포가 정규분포에 가까워지며, 이를 통해 모집단 평균을 보다 정확히 추정할 수 있습니다. 이 과정에서 표준오차는 중요한 역할을 합니다.
표준오차와 표본 편차의 차이점
표준오차 (Standard Error, SE)
정의:
표본 평균의 변동성을 측정하는 지표로, 표본 평균이 모집단 평균에 얼마나 가까운지를 나타냄.
목적:
추정치(예: 표본 평균)의 정확도를 평가하는 데 사용됨.
계산식:
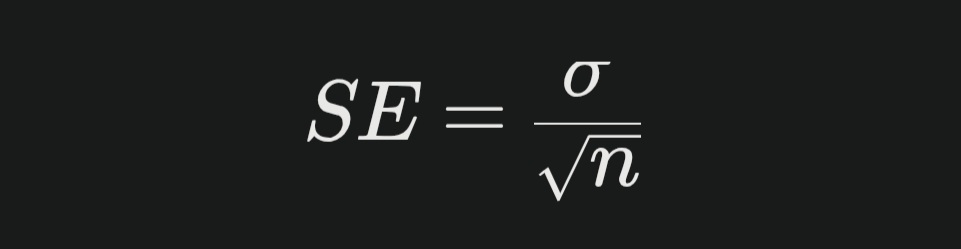
특징
표본 크기가 클수록 표준오차는 작아짐.
모집단 평균 추정치의 신뢰성을 판단하는 데 유용함.
표본 편차 (Sample Standard Deviation, s)
정의:
표본 내 데이터 값들의 흩어짐을 측정하는 지표로, 각 데이터가 평균값에서 얼마나 떨어져 있는지를 나타냄.
목적
표본 자체의 분산 정도를 평가하는 데 사용됨.
계산식
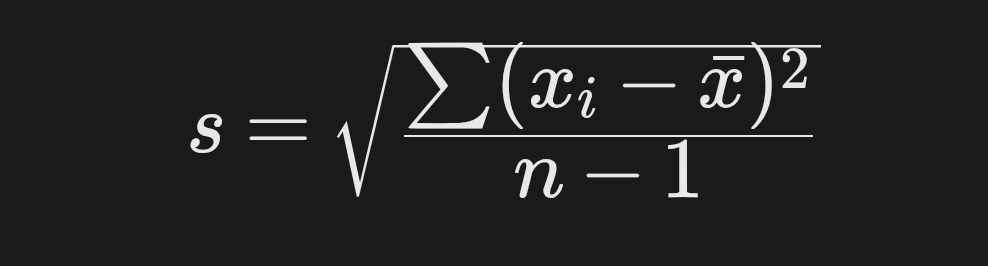
특징
데이터가 평균값에 가까울수록 표본 편차는 작아지고, 흩어져 있을수록 커짐.
단일 표본 내의 데이터 분포를 설명함.
주요 차이점
표준오차는 추정치(예: 평균)의 신뢰성을 나타내며, 주로 모집단에 대한 추론에 사용됨.
표본 편차는 데이터의 흩어진 정도를 나타내며, 주로 표본 자체를 설명하는 데 사용됨.
'평균과 통계기반 사회정보' 카테고리의 다른 글
| 베트남 내 한국 기업 생산공장 삼성전자 현대차 한화비젼 LG전자 위치 지도 (10) | 2025.04.04 |
|---|---|
| 국내 체류 재외동포 40%가 60대 고령화 지속 : 최근 5년간 재외동포중 60대이상 비율통계 (4) | 2025.04.04 |
| ICT 자격증 인기 급상승! 5년간 응시자 연평균 8% 증가 #ICT자격종류 (2) | 2025.04.02 |
| 윤석열 대통령 탄핵 심판 선고일시 및 관련 주요 내용 (2) | 2025.04.01 |
| LGBTQ 뜻 LGBTQIA 용어정의 약어 역사적 이정표 조사결과 (12) | 2025.03.31 |



